
Kleiner Resonanzwandler (30W)

Dies hier ist, bzw. war mein erster Versuch, einen Spannungswandler mit nachgeschalteter Kaskade zu bauen. Eine Weile lang hat das Teil wunderbar funktioniert, bis von der unteren Doppelreihe aus Kondensatoren Funken in den Transformator schlugen. Dieser hat jetzt eine durchgebrannte Wicklung und ist nur noch als Briefbeschwerer zu gebrauchen.
Dieser Wandler hatte eine Leistung von ca. 30W bei 4kV Ausgangsspannung. Es war damit möglich, ein 1,6mW HeNe-Laserrohr zu betreiben.
Bevor mit den ernsthaften Experimenten, die im Vorwort erwähnt werden, begonnen werden kann, muß erst mal eine passende Stromversorgung her. Wie man sich sowas selbst bauen kann, wird im Folgenden erklärt.
Dimensionierung des Transformators:
Dimensionierung der Bauelemente:
Transistoren und Vorwiderstände
Daß dieses Gerät bereits nach wenigen Betriebsminuten den Weg alles irdischen ging, liegt weder am Funktionsprinzip, noch an der Dimensionierung der Bauelemente. Der Apparat brannte ab, weil die hohe Spannung nicht ausreichend isoliert wurde. Anfänglich war nur die obere, dreistufige Kaskade an den Transformator angeschlossen, und so lange arbeitete der Wandler auch tadellos. Der Wandler, der dem hier beschriebenen nachfolgen soll, wird zwar erheblich ernsthafter (und größer) konstruiert sein, aber auf demselben Funktionsprinzip beruhen. Vor Überraschungen wird man aber leider (und glücklicherweise) niemals sicher sein! :-P
Im Folgenden wird zuerst der Wandler beschrieben, der die Eingangsspannung für die nachfolgende Villard-Kaskade erzeugt. Der Wandler alleine ist recht universell und kann für eine Vielzahl von Hochspannungsexperimenten, wie z.B. für Gasentladungen verwendet werden.
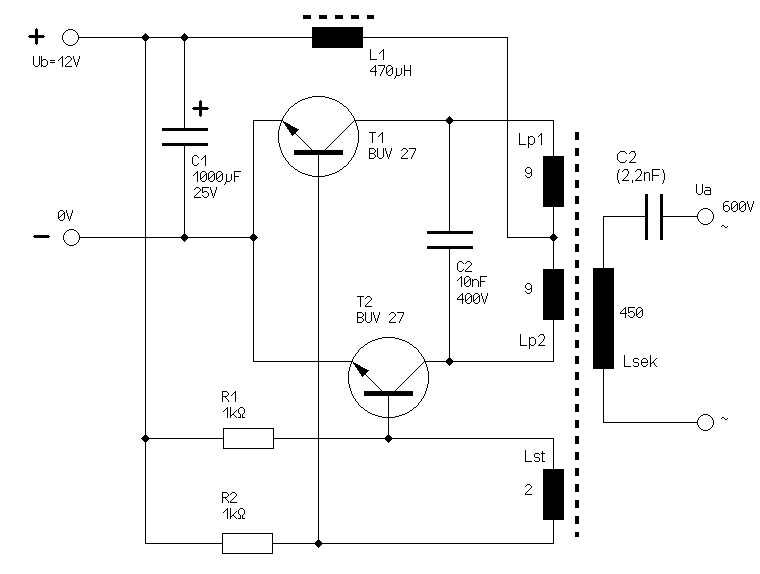
Die Schaltung erscheint simpel, aber sie hat's in sich!
Es handelt sich hier um einen Gegentaktwandler, d.h. die beiden Transistoren schalten abwechselnd. Das Tastverhältnis, mit dem die Transistoren angesteuert werden, liegt immer bei 50%. Durch die gegensätzlichen Wickelsinne der beiden Primärspulen wird der Kern des Transformators für beide Magnetisierungsrichtungen genutzt. Dadurch wird der Trafo wesentlich besser ausgenutzt, als bei Wandlern, die den Kern nur in eine Richtung aussteuern (z.B. Sperr- Durchflußwandler). Das Grundprinzip ähnelt übrigens dem eines Tesla-Transformators, nur daß bei einem solchen die Anregung des Primärkreises eher unkontrolliert durch eine Funkenstrecke erfolgt.
Der Kondensator C2 bildet zusammen mit den Primärwicklungen den Primärschwingkreis. Die Resonanzfrequenz des Primärschwingkreises tritt nur dann auf, wenn die Schaltung entweder im Leerlauf, oder bei sehr geringer Last betrieben wird.
Wird auf der Sekundärseite des Transformators eine kapazitive Last (z.B. eine Vervielfacherkaskade) angeschlossen, bildet diese zusammen mit der Sekundärspule einen weiteren Schwingkreis. Je größer der Strom in der Sekundärspule dann wird, desto mehr übernimmt der Sekundärkreis die "Kontrolle" über die Schwingfrequenz.
Die Spule L1 speist den Wandler mit konstanten Strom. Ohne diese Spule würde der Wandler zwar auch arbeiten, jedoch wird dann das Lastverhalten deutlich schlechter und der Wandler erzeugt keine sinusförmige Spannung mehr.
Die Steuerwicklung auf dem Trafo, bestehend aus zwei Windungen, ist dafür zuständig, daß die Transistoren beim Nulldurchgang der Sinusschwingung umgeschaltet werden. Die Steuerwicklung besteht nur aus wenigen Windungen (2...4), da die beiden Transistoren nicht viel Spannung (0,7V) benötigen um aufgesteuert zu werden.
Die beiden Widerstände sorgen im Einschaltmoment dafür, daß die Transistoren überhaupt anfangen können zu leiten, und im normalen Betriebsfall leiten sie „überschüssigen“ Strom aus der Steuerwicklung ab.
Da die beiden Transistoren schaltend betrieben werden, ist deren Verlustleistung recht gering. Daher kamen sie in dieser Schaltung auch ohne Kühlkörper aus.
Die Ausgangsspannung der Schaltung hängt nur von der Windungszahl der Sekundärspule ab. Theoretisch sind bei entsprechend gewählter Windungszahl beliebig hohe Spannungen möglich. Die vergleichsweise geringe Ausgangsspannung des Transformators von 600Veff wurde gewählt um die Kondensatoren der nachfolgenden Kaskade, die maximal 650Veff aushalten, nicht zu überlasten.
Dimensionierung des Transformators (< zur Übersicht)
Da der Transformator gewissermaßen das "Herz" der Schaltung darstellt, wird mit dessen Dimensionierung begonnen. Die Dimensionierung von Ferrit-Transformatoren ist zwar etwas aufwendig, jedoch werden keine besonderen Anforderungen an die mathematischen Fähigkeiten des Entwicklers/Bastlers gestellt. Mit einer handvoll leicht berechenbarer Formeln kommt man aus. Die (Ent-)Wicklung von solchen Trafos ist keine exakte Wissenschaft, es gibt keine Formel in die man die Wunschwerte einsetzt und dann sämtliche Daten für das ganze Teil herausbekommt. Will man die Sache gründlich angehen, muß viel hin und her gerechnet werden, bis das Ding endlich fertig ist. Nun, diese Seite richtet sich hauptsächlich an Hobby-Experimentatoren, weshalb es im Folgenden nicht so tierisch genau genommen werden soll. ;-)
In der weiteren Entwicklung (weiter unten auf dieser Seite) wird sich ohnehin herausstellen, daß, bedingt durch die Schwingkreiskonstruktion wieder andere Werte auftreten als zuerst berechnet. Auch deswegen wären für eine gründliche Entwicklung viele Versuche mit ausladenden Rechnereien nötig.
Es wurde ein E25-Kern aus N67-Material mit 0,5mm Luftspalt des Herstellers EPCOS verwendet, weil dieser Transformatorkern gerade passend verfügbar war. (Das ist das Schöne am Basteln - man muß sich nicht an ein Pflichtenheft halten und kann Teile verwenden, die noch irgendwo herumliegen. Daher kriegen auch Bastler eine Schaltung meistens schneller fertig als Profis. ;-) Das N67-Material wird zwar nicht mehr hergestellt, aber das aktuelle N87-Material eignet sich mindestens genausogut.
Aus dem Datenblatt dieses Ferritkerns sind folgende Daten zu entnehmen:
AL-Wert
bei 0,5mm Luftspalt = 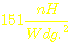
Maximale Flußdichte: B,max = 200 mT
Maximale Frequenz f,max = 100kHz
Eisenquerschnitt
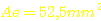
Verfügbarer Wickelraum: 16mm Breite * 3,8mm Höhe (zu entnehmen aus der Zeichnung des Spulenkörpers)
Windungszahlen: (< zur Übersicht)
Nach der
Transformatorgleichung:
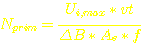
Suchen wir uns mal die Variablen zusammen um die benötigte Primär-Windungszahl ausrechnen zu können:
B:
Der
Kern wird in beide Richtungen ausgesteuert, daher ist 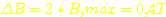
Ui,max ist die maximale Spannung, die an einer der Primärspulen im Betrieb des Wandlers anliegt. Diesen Wert theoretisch zu bestimmen ist bei der vorliegenden Schaltung nicht ganz einfach. Einerseits sorgen Verluste in der Schaltung (Spannungsabfälle an Verpolschutzdiode, Drosselspule und Transistoren) für eine Reduzierung dieser Spannung, andererseits erreicht durch den Schwingkreis an den Primärspulen die Spannung wieder höhere Werte. Wird die Spannung in der realen Schaltung höher als berechnet, steigen die Verluste im Transformatorkern. Dies ist in aller Regel aber zu verschmerzen. Sollte sich herausstellen, daß der reale Spannungswert um mehrere Volt von der Berechnungsgrundlage abweicht, sollte die Berechnung der Windungszahlen erneut durchgeführt und ein neuer, angepaßter Trafo gewickelt werden.
Ui,max:
Näherungsweise wird jetzt behauptet: 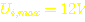 (gewählt. 12V-Technik kenne ich schon ganz gut ;)
(gewählt. 12V-Technik kenne ich schon ganz gut ;)
vt: Das Tastverhältnis. vt = 50% (ist bei dieser Art von Wandler immer so)
f: Frequenz f = 30kHz (geringe Frequenz => guter Wirkungsgrad bei "langsamen" Transistoren)
Ae:
Der
Eisenquerschnitt der Kerns (Fläche, die vom Magnetfeld durchflutet wird)

Also brauchen
wir für jede der beiden Primärspulen: 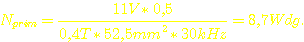
Gewählt: 9 Windungen
Denn es gibt keine halben oder dreiviertels Windungen. ;) Versucht man, eine dreiviertels Windung mechanisch irgendwie an den Spulenkörper des Transformators hinzudrappieren, erhöht man höchstens das Streufeld, wodurch der Transformator größere Verluste produziert. Durch die Wahl von 9 Wdg. statt 8 wird der Trafokern weniger stark ausgesteuert und die Verluste werden verringert.
Die beiden Primärspulen sollten möglichst gleich sein, damit Unsymmetrien vermieden werden. Die beiden Primärspulen mit jeweils 9 Windungen werden bifilar, d.h. miteinander gewickelt. Dadurch wird sichergestellt, daß beide Wicklungen dieselbe Induktivität, und dieselbe Kopplung zum Kern haben.
Um die Windungszahl der Sekundärspule des Transformators berechnen zu können, brauchen wir das Übersetzungsverhältnis, das der Trafo haben soll. Da die Kondensatoren der nachfolgenden Vervielfacherkaskade (Beschreibung folgt) 650V Wechselspannung aushalten, soll die Ausgangsspannung 600V betragen. Damit haben wir noch einen kleinen Sicherheitsabstand bis zur Grenze, die die Spezifikation der Kondensatoren vorgibt.
Das
Übersetzungsverhältnis berechnet sich folgendermaßen: 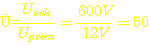
Dann
muß die Sekundärspule 50-mal soviele Windungen haben wie eine der
Primärspulen: 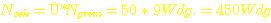
Die Steuerwicklung muß genug Spannung erzeugen um die beiden Transistoren T1,T2 umzuschalten, sie liefert aber prinzipiell eine sinusförmige Spannung. Wünschenswert wäre hier aber eine rechteckförmige Spannung, da die Transistoren ja "knackig" geschaltet werden sollen. Werden die Transistoren hier, wie in einem Niederfrequenzverstärker, nur linear auf- und zu-gesteuert, produzieren sie unnötigerweise hohe Verluste. Ein Siliziumtransistor schaltet ein, wenn seine Basis +0,7V erreicht.
Eine
der Primärspulen des Transformators hat 9 Windungen und es liegen 12V an
ihr an, das ergibt dann eine Spannung von 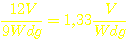 . Das heißt, daß an einer einzigen Windung eine Effektivspannung
von 1,33V anliegt. Durch den sinusförmigen Verlauf der Spannungen im Trafo
werden jedoch die 0,7V, die benötigt werden, bei einer einzigen Windung
zu langsam, bzw. zu spät erreicht. Aus Versuchen ergab sich, daß
die Schaltung am Besten funktioniert, wenn die Steuerwicklung zwei Windungen
hat. Mit einer größeren Windungszahl steigen die Verluste. Wenn jemand
diese Windungszahl rechnerisch optimieren will, so wünsche ich ihm viel
Spaß dabei! :-D
. Das heißt, daß an einer einzigen Windung eine Effektivspannung
von 1,33V anliegt. Durch den sinusförmigen Verlauf der Spannungen im Trafo
werden jedoch die 0,7V, die benötigt werden, bei einer einzigen Windung
zu langsam, bzw. zu spät erreicht. Aus Versuchen ergab sich, daß
die Schaltung am Besten funktioniert, wenn die Steuerwicklung zwei Windungen
hat. Mit einer größeren Windungszahl steigen die Verluste. Wenn jemand
diese Windungszahl rechnerisch optimieren will, so wünsche ich ihm viel
Spaß dabei! :-D
So, die Windungszahlen hätten wir schon mal, fertig sind wir aber immer noch nicht. Es fehlen noch die benötigten Drahtstärken, bzw. -durchmesser.
Drahtstärke: (< zur Übersicht)
Für den Drahtdurchmesser gilt:
- Je größer, desto geringer die Verluste
- Je kleiner, desto weniger Wickelraum wird benötigt. (Der Drahtwickel muß ja noch auf den Spulenkörper passen)
==> Es muß ein vernünftiger Kompromiß zwischen akzeptablen Verlusten durch den ohmschen Widerstand des Drahtes und der Füllung des Spulenkörpers gefunden werden.
Die
Formel für die Stromdichte S in Leitern lautet: 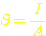 =>
=> 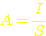
S:
Stromdichte
in 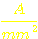
I: Strom in A
A:
Drahtquerschnitt, bzw. Fläche in 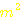
Mit
der Formel für die Kreisfläche: 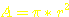 =>
=> 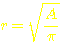 =>
=> 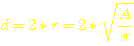 bekommen wir den benötigten Drahtdurchmesser heraus.
bekommen wir den benötigten Drahtdurchmesser heraus.
d: Durchmesser in m
r: Radius im m
Der
Wandler soll 30W haben, und mit 12V versorgt werden. Das ergibt einen Strom
von 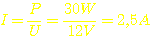 für beide Primärspulen. Also bekommt jede Primärspule
nur die Hälfte des gesamten Stromes ab: 1,25A.
für beide Primärspulen. Also bekommt jede Primärspule
nur die Hälfte des gesamten Stromes ab: 1,25A.
Eine
gute Faustwert für Drähte auf kleinen Ferrittransformatoren ist: 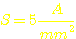 .
.
Wir
haben einen Strom von 1,25A, also brauchen wir einen Drahtquerschnitt (A) von:
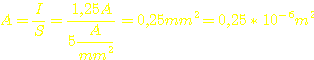
Das
ergibt dann einen Drahtdurchmesser von: 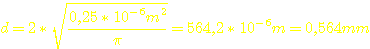
Der Draht in meiner Bastelkiste, der am nächsten an den errechneten Wert herankommt, hat 0,5mm Durchmesser. Also wird auch genau dieser verwendet. ;-)
Die Primärspule besteht aus 2*9 Windungen. Nebeneinandergewickelt ergibt das eine Breite von: 18*0,5mm = 9mm. Der Spulenkörper hat, wie im Datenblatt angegeben, eine Breite von 16mm, also passen die beiden Primärspulen noch wunderbar auf eine einzige Wicklungslage. Das ist ganz hervorragend, denn hätte man eine zweite Lage anfangen müssen, wäre relativ viel Wickelraum auf dem Spulenkörper verbraucht worden. Immerhin ist der Draht ja ganze 0,5mm "dick". Die Primärspule ist jetzt (endlich) fertig berechnet.
Die Sekundärspule wird schon deutlich größer, wie folgende Rechnerei zeigen wird, denn schließlich hat sie 450 Windungen und nicht nur 9. Dieser Spule soll bei 600V eine Leistung von 30W (bzw. VA) entnommen werden können.
Folglich muß diese Spule einen Strom von 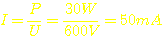 aushalten.
aushalten.
Mit obigem Faustwert für die Stromdichte von 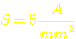
bekommen wir hier einen Drahtquerschnitt (Fläche) von 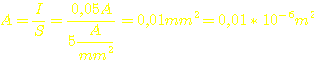
Der
benötigte Drahtquerschnitt ist dann: 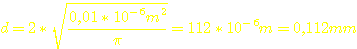
Der nächstliegende Wert (liegend in der Bastelkiste) ist 0,2mm, und dieser Draht soll auch verwendet werden. Abgesehen von der besseren Verfügbarkeit hat dieser Draht auch den Vorteil, daß er nicht ganz so dünn ist, wie 0,1-er Draht. Superdünner Draht ist äußerst lästig, und schwierig (sauber) zu wickeln. Außerdem werden durch dickeren Draht auch die ohmschen Verluste kleiner. Wenn also 450 Windungen 0,2mm-Draht auf den Spulenkörper passen, haben wir gewonnen. Schau'mer mal...
Der
Spulenkörper ist 16mm breit, also passen 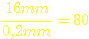 Windungen nebeneinander auf eine Wicklungslage. Da man aber nie 100%-ig
sauber wickeln kann, werden es in der Praxis immer etwas weniger sein. Gehen
wir mal von 75 Wdg./Lage aus. Will man einen Hochspannungstransformator wickeln,
ist es sehr zu empfehlen, jeweils an Wicklungsanfang und -ende etwas Platz zu
lassen. Sonst kann es passieren, daß im Betrieb Überschläge
zwischen den Lagen auftreten. Schätzen wir also nochmals 5 Windungen pro
Lage weg, dann haben wir jetzt 70 Wdg./Lage.
Windungen nebeneinander auf eine Wicklungslage. Da man aber nie 100%-ig
sauber wickeln kann, werden es in der Praxis immer etwas weniger sein. Gehen
wir mal von 75 Wdg./Lage aus. Will man einen Hochspannungstransformator wickeln,
ist es sehr zu empfehlen, jeweils an Wicklungsanfang und -ende etwas Platz zu
lassen. Sonst kann es passieren, daß im Betrieb Überschläge
zwischen den Lagen auftreten. Schätzen wir also nochmals 5 Windungen pro
Lage weg, dann haben wir jetzt 70 Wdg./Lage.
Zwischen den Wicklungslagen muß eine Isolierschicht eingefügt werden. Ich habe bisher mit 0,1mm starkem Teflonband sehr gute Erfahrungen gemacht, also wird es auch hier zur Anwendung gebracht. Solches Band gibt es in der Sanitärabteilung in Baumärkten. Man verwendet es normalerweise zur Abdichtung von Rohrverschraubungen. Eine Lage Teflonband reicht nicht aus, da sonst kleine Spalte zwischen den Wicklungslagen (aus Teflonband) auftreten. An solch einem Spalt könnte ein elektrischer Überschlag zwischen zwei Wicklungen auftreten. Das Teflonband muß überlappend auf jede gerade fertige Draht-Lage gewickelt werden. Jede Isolier-Lage ist mit 0,2mm also genauso dick wie der Wickeldraht selber.
Bei
70 Windungen pro Lage brauchen wir also 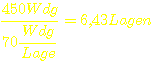 .
.
Verbraucht wird also Wickelhöhe für 7 Lagen Draht + 7 Lagen Teflon. Die Wicklung wird also 7*0,2mm + 7*0,2mm = 2,8mm. dick, bzw. hoch.
Addiert man nun die Wickelhöhen der beiden bisher ausgerechneten Wicklungen (primär und sekundär), kommt man auf:
0,5mm + 2,8mm = 3,3mm. Laut Datenblatt des Trafokerns (Spulenkörpers) haben wir 3,8mm Höhe zur Verfügung, und der ganze Kram paßt noch drauf. (Glück gehabt!)
Die Steuerwicklung mit ihren zwei Windungen kann man noch irgendwo "reinwurschteln" - anders gesagt: Dafür ist sicher noch Platz. Diese Wicklung muß nur den relativ kleinen Basisstrom für die beiden Schalttransistoren T1 und T2 liefern. Hierfür reicht (Pi * Daumen) 0,2mm-Draht aus.
Induktivitäten der Wicklungen (< zur Übersicht)
So, die meisten Daten des Transformators haben wir jetzt zusammen, es fehlen aber noch die Induktivitäten der Primär- und Sekundärspule. Diese lassen sich wie folgt ausrechnen:
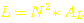
L: Induktivität in H (Henry)
N: Windungszahl (ohne Einheit)
AL:
AL-Wert
in 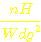 (aus der Angabe im Datenblatt, hier 151
(aus der Angabe im Datenblatt, hier 151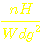 )
)
Damit
bekommen wir für eine der beiden Primärspulen eine Induktivität
von 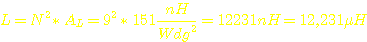
Beide Primärspulen sind in Reihe geschaltet und liegen auf demselben Kern, sind also magnetisch gekoppelt. Nach obiger Formel quadriert sich die Induktivität wenn sich die Windungszahl verdoppelt. Also bedeutet die doppelte Windungszahl die vierfache Induktivität. Das wären dann 48,9µH. Wer's nicht glaubt, darf gerne nachrechnen. :-D
Jetzt
fehlt noch die Induktivität der Sekundärspule: 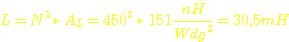
Jetzt könnte man noch die Induktivität der Steuerwicklung ausrechnen, da dieser Wert aber überhaupt nicht interessiert, kann man sich das sparen.
Die Induktivitäten, die hier ausgerechnet wurden, werden für die Berechnung der Schaltung benötigt. Mehr dazu weiter unten.
Gesammelte Daten: (< zurück zur Übersicht)
Bisher haben wir folgende Werte des Transformators ermittelt:
Primär (Niederspannungs-Eingangsseite):
Wicklung:
2 * 9 Wdg;  0,5mm
0,5mm
Induktivität: Lprim = 2 (*) 12,2µH, ergibt 48,9µH insgesamt
Eingangsspannung: 12 Veff
Eingangstrom: 2,5 A=
Sekundär (Hochspannungs-Ausgangsseite):
Wicklung:
450 Wdg auf 6,5 Lagen à 70 Wdg 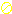 0,2mm
0,2mm
Induktivität: L = 30,5mH
Ausgangsspannung: 600Veff
Ausgangsstrom: 50mA
Damit wären wir mit der Berechnung des Transformators (endlich) fertig! :o
Dimensionierung der Bauelemente: (< zur Übersicht)
Nachdem der Transformator soweit berechnet ist, fehlen noch die übrigen Bauteile. Deren Berechnung, bzw. Auswahl/Dimensionierung ist bei Weitem nicht mehr so aufwendig. Fangen wir mal mit den Teilen an, die den Strom zwischen den beiden Primärspulen hin und her schalten sollen, den Transistoren also.
Transistoren und Vorwiderstände (< zur Übersicht)
Für die Schalttransistoren wurde der Typ BUV27 (npn) des Herstellers ST (SGS-Thomson) gewählt. Aus dem Datenblatt sind folgende Werte zu entnehmen:
Maximale Kollektorspannung: UCE,max = 120V
Maximaler Kollektorstrom: 12A
Maximale Sperrspannung der Basis-Emitter-Strecke: 7V (Unsere Steuerwicklung auf dem Trafo erreicht nicht einmal die Hälfte davon -> keine Gefahr)
Leider brachte es der Hersteller in seinem spartanischen Datenblatt nicht fertig, den Wert für die Stromverstärkung (B) des Transistors anzugeben. Da diese wichtige Angabe fehlt, müssen die Werte für die Basisvorwiderstände R1 und R2 "hinprobiert" werden. Ohne diese Angabe muß der Versuch einer Berechnung scheitern. Glücklicherweise ist der Transistor weitaus besser als das zugehörige Datenblatt.
Es ist nicht zwingend erforderlich, derart leistungsstarke Transistoren für den hier zu konstruierenden Wandler zu verwenden, jedoch bringt die Verwendung überdimensionierter Transistoren einige Vorteile mit sich:
Die maximale Kollektorspannung von 120V wird in der vorliegenden Schaltung niemals erreicht, nicht einmal dann, wenn man die Betriebsspannung auf einen Wert von deutlich über 12V aufdreht. Selbst 24V bringen die Schaltung noch nicht um, sie wird nur wärmer. So wird die Schaltung sehr robust, was für die Durchführung ernsthafter Experimente ein nicht zu unterschätzender Vorteil ist.
Werden die Transistoren mit einem Kollektorstrom betrieben, der weit unter deren Maximalwert liegt, haben sie eine ziemlich hohe Verstärkung. Diese ist im vorliegenden Fall (IC=2,5A ) schätzungsweise um den Faktor 4 höher als bei maximaler Belastung mit 12A. Dadurch können relativ hochohmige Vorwiderstände verwendet werden, was dem Wirkungsgrad der Schaltung zugute kommt, außerdem schalten die Transistoren in dieser Schaltung schneller, wenn sie eine hohe Verstärkung haben - auch das verbessert den Wirkungsgrad der Schaltung. Ich schätze mal die Verstärkung der BUV27 bei dieser geringen Belastung auf ca. 80; nachgemessen habe ich sie jedoch nicht.
Dadurch, daß die Transistoren nur auf "kleiner Flamme" laufen, produzieren sie auch nur sehr wenig Wärme, weshalb man sich in vorliegender Schaltung Kühlkörper sparen kann. Das vereinfacht den Aufbau, bzw. Nachbau des Gerätes. Die Transistoren werden gerade mal lauwarm.
Die Basis-Vorwiderstände der Transistoren wurden auf 1k Ohm hinprobiert. Somit bekommt jeder der beiden BUV27 einen Basisstrom von knapp 12mA plus dem Strom, den die Steuerwicklung auf dem Transformator liefert. Die Schaltung läuft wunderbar damit. Da der Transformator einen Luftspalt (magnetischer Widerstand) besitzt, welcher den Strom begrenzt, erreicht der Basisstrom keine gefährlichen Werte.
Schwingkreis und Frequenz (< zur Übersicht)
Schwingkreise (primär und sekundär)
Der Schwingkreis auf der Primärseite besteht aus den beiden Primärspulen des Transformators und dem Kondensator C2. Auf der Sekundärseite haben wir einen Schwingkreis aus Lsek und C3.
Für Die Resonanzfrequenz gilt die Thomson'sche Schwingungsformel:
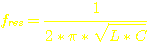
fres: Resonanzfrequenz des Schwingkreises in Hz
L: Induktivität in Henry (des Primärschwingkreises)
C:
Kondensator ( ) in Farad
) in Farad
Mit den Werten, die in obigem Schaltplan stehen und der Induktivität der Primärspulen für den Transformator haben wir:
C2 = 10nF; Lprim= 48,9µH
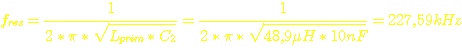
Diese Frequenz erscheint ziemlich hoch, wenn man bedenkt, daß der Kern des Transformators nur für 100kHz spezifiziert ist. Diese Frequenz tritt aber nur im Leerlauf auf, also wenn der Ausgang des Wandlers nicht belastet wird. In diesem Betriebszustand verbraucht der Wandler wegen der Wirbelstromverluste im Ferritkern einen relativ hohen Leerlaufstrom (ca. 100mA).
Wenn die Schaltung jedoch belastet wird, gewinnt der Sekundarschwingkreis immer mehr die "Oberhand", d.h. je stärker der Wandler ausgangsseitig belastet wird, desto verschiebt sich die Frequenz des Wandlers in die Nähe der Frequenz, die sich aus dem Schwingkreis auf der Sekundärseite ( C3 = 2,2nF , Lsek = 30,5mH ) ergibt.
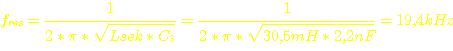
Je nach Belastung verschiebt sich die Frequenz also zwischen 227,5 kHz und 19,4kHz. Eine derart große Frequenzänderung ist nicht gut, da sich dadurch das Verhalten des Wandlers über die Frequenz sehr stark ändert. Diese 19,4 kHz sind eigentlich viel zu niedrig. Bei derart niedriger Frequenz ist die Leistung des Wandlers viel kleiner als sie sein könnte. Spätestens jetzt bemerkt man, daß dieser kleine Wandler gebaut wurde, ohne zuvor ausreichend genau berechnet worden zu sein. :-P
Nun ja, das Ding funktioniert trotzdem und als Berechnungs- wie Dimensionierungsbeispiel kann es immer noch dienen. Also machen wir einfach weiter. ;-)
Die obige Berechnung hat noch eine Lücke. An dem Transformator befinden sich schließlich zwei Schwingkreise und nicht nur einer. Um die genaue Frequenz zu bestimmen, müssen beide Schwingkreise zu einem einzigen zusammengerechnet werden. Die Kapazität auf der Primärseite wird dafür mittels des Übersetzungsverhältnis des Transformators auf die Sekundärseite übertragen. Das geht folgendermaßen:
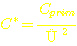
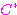 = Auf die Sekundärseite transformierte
Kapazität in Farad
= Auf die Sekundärseite transformierte
Kapazität in Farad
Cprim = Kondensator auf der Primärseite (hier: C2) in Farad
Ü = Übersetzungsverhältnis des Transformators (Faktor ohne Einheit)
Ausgerechnet
heißt das: 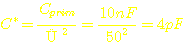
Okay, diese 4 pF können wir eigentlich getrost ignorieren, das ist verglichen mit den 2,2nF der Kaskade praktisch nichts mehr. Hätte C2, bzw C* eine nennenswerte Kapazität, müßte dessen Einfluß auf die Resonanzfrequenz im Lastfall berücksichtigt werden. Dazu würde man den berechneten C* auf die Kapazität im Sekundärkreis C3 dazuaddieren und die daraus resultierende Resonandfrequenz berechnen. In jedem Fall gilt, daß die Kapazität auf der Primärseite ebenfalls die Frequenz des Wandlers verringert. Nur der Vollständigkeit halber soll diese Berechnung hier durchgeführt werden.
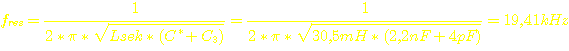
=> Es ändert sich in diesem Fall praktisch nichts.
Leistung des Wandlers (< zur Übersicht)
Der
Kondensator mit dem der Wandler belastet wird, ist die Eingangskapazität
der Kaskade. Diese hat bei der Arbeitsfrequenz von 19,4 kHz einen Blindwiderstand
von: 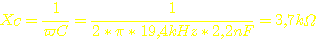
Bei
der Ausgangsspannung von 600V ergibt das einen Ausgangsstrom von: 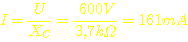
Mit der Spannung von 600V und dem Strom von 161mA erhalten wir eine Scheinleistung des Transformators, bzw. des Wandlers von
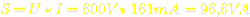
S: Scheinleistung des Wandlers in VA
Scheinleistung (S) und Wirkleistung (P) dürfen nicht verwechselt werden, daher erhält die Scheinleistung die Bezeichnung "VA" und nicht "W". Ist der Wandler in Betrieb, tritt die Scheinleistung immer auf. Obwohl die Ströme und Spannungen (161mA und 600V) in dieser Schaltung in jedem Betriebszustand gemessen werden können, nimmt der Wandler nicht ständig die o.g. Scheinleistung aus der Spannungsversorgung (12V Gleichspannung) auf. In den Schwingkreisen auf Primär- und Sekundärseite "schwappt" ständig Energie zwischen Kondensatoren und Spulen hin und her. Aus dem Energiegehalt von den Transformatorwicklungen und den Kondensatoren ergibt sich, zusammen mit der Frequenz, die Scheinleistung des Wandlers. Erst, wenn der Wandler ausgangsseitig belastet wird, nimmt dieser Wirkleistung (P in W) primärseitig auf, und gibt sie sekundärseitig wieder ab.
U,I: Beträge der Effektivwerte von Strom und Spannung in V, bzw. A, ohne Rücksicht auf die Phasenlage zueinander.
Eingangsfilter (< zur Übersicht)
Dieser Wandler muß mit annähernd konstantem Strom betrieben werden damit er richtig funktioniert. Der Gleichstrom, der am Verbindungspunkt zwischen Lp1 und Lp2 eingespeist wird, wird von der Drosselspule L1 konstant gehalten. Diese Spule muß so dimensioniert werden, daß trotz der Wechselspannung die über ihr anliegt ein konstanter Strom durch sie fließt. Die Wechselspannung über der Drossel verursacht eine gewisse Welligkeit des Stromes - je größer die Spule, desto kleiner ist diese Welligkeit.
Der Wandler funktioniert schon mit einer sehr kleinen Drossel (ca. 100µH), aber dann ist diese Stromwelligkeit noch relativ groß, und der Elko, der die Versorgungsspannung glättet, wäre möglicherweise überfordert. Die hier verwendete Drossel hat eine Induktivität von 470µH, also hat sie bei f = 19,4kHz einen Blindwiderstand von:
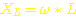
XL = induktiver Blindwiderstand in Ohm
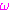 =
Kreisfrequenz (
=
Kreisfrequenz (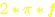 ) in 1/sec
) in 1/sec
L = Induktivität in Henry
Das
ergibt also einen Blindwiderstand von: 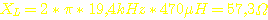
Dieser Blindwiderstand wirkt nur für die Wechselspannung, bzw. den Wechselstrom. Der speisende Gleichstrom wird von diesem Blindwiderstand nicht beeinflußt. Daher wirkt L1 auch als Filterdrossel.
Über L1 liegt eine Wechselspannung in der Höhe der Betriebsspannung an, also 12Veff. Mit dieser Spannung und dem Blindwiderstand können wir jetzt ausrechnen, wie groß der Anteil des Wechselstromes ist, der durch die Drossel fließt.
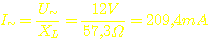
Diese 209,4 mA werden jetzt dem Elektrolytkondensator C1 aufgebrummt. Da es sich bei diesem um einen recht großen Brocken handelt, sollte dieser Wechselstrom kein Problem für ihn darstellen. Mit diesem Filter aus L1 und C1 sollte man den Wandler an so ziemlich jeder Spannungsquelle betreiben können, ohne daß diese durch den Wandler gestört wird.
Damit sollte dieser Schaltwandler ausreichend beschrieben sein. Die Funktionsweise einer Hochspannungskaskade soll später, bzw. woanders beschrieben werden.
Wer Schreibfehler findet, darf sie behalten. Bei inhaltlichen Fehlern, bitte eine Email an mich.
Zusatz (7.7.03) (< zur Übersicht)
Zugegebenermaßen gibt obige Beschreibung nicht die ganze Wahrheit wieder. Die Thematik ist in Wirklichkeit etwas komplexer als oben dargestellt. Es wurden, vor allem bei der Berechnung des Transformators, einige Näherungen verwendet, die bei leistungsstärkeren Wandlern nicht mehr verwendet werden können.
Warum schreibe ich das erst jetzt und nicht schon früher? Ganz einfach: Ich wußte das vorher selber noch nicht. :p Erst bei der Berechnung einiger Details eines sehr ernsthaften Netzgerätes (seNG!) stellte sich heraus, daß die kleinen Ungenauigkeiten, die in obigen Berechnungen enthalten sind, sich bei hohen Leistungen (kW-Bereich) und höheren Eingangsspannungen (Netz) ungünstig auswirken.
Dies sei hier nur der Vollständigkeit und der Korrektheit halber erwähnt. Der kleine Wandler kann also mit oben beschriebenen Methoden hinreichend genau dimensioniert werden.