Zurück zur Hauptseite

Zurück zum Projektverzeichnis

< Vorige    Nächste >

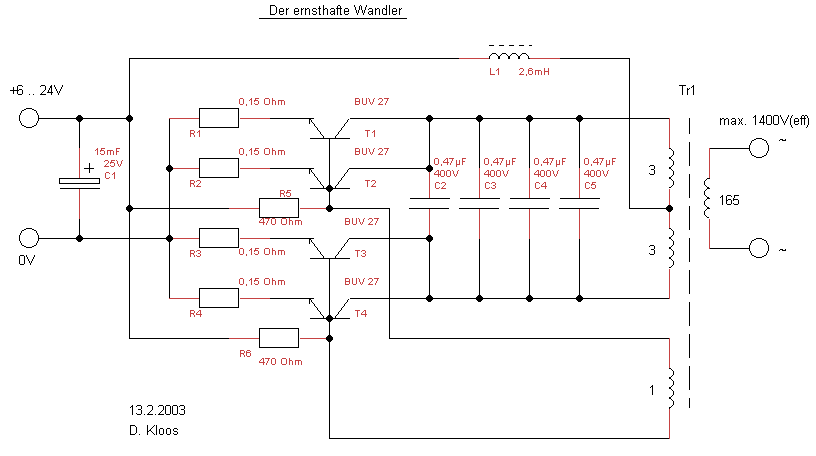
 Der ernsthafte Wandler

(Time to get serious!)

Übersicht:

Kurzbeschreibung

Schaltplan:

Stückliste mit Datenblättern

Beschreibung des Ganzen

 Der ernsthafte Transformator

Primärschwingkeis und Kondensatoren

Transistor-Schaltstufen

Die dicke L1

Berechnung der real existierenden Spule

Berechnung der korrekten Spule

Inbetriebnahme

Das allererste Mal

Anschluß des Transformators

Nachwort

Der ernsthafte Wandler, dessen Realisierung bereits in der Beschreibung des kleinen Wandlers prophezeiht wurde, ist nun Realität geworden! Das Funktionsprinzip dieses Apparates ist dasselbe, wie vorher, nur wurden diesmal einfach die Bauteile deutlich größer dimensioniert und neu berechnet. Die maximale Leistung dieses Gerätes ist so ungeheuer, daß sie bis zum jetzigen Zeitpunkt noch nicht einmal experimentell ermittelt werden konnte! (Mein Labornetzgerät bringt nur 5A :-P) Rechnerisch sollten ca. 500 VA drin sein.

Kurzbeschreibung

(< zur Übersicht)

Technische Daten (theoretisch):

Funktionsprinzip: Gegentakt-Resonanzwandler

Leistung: 500 VA

Eingang: 4-25V / 20 A

Ausgang: 220-1400V / 364 mA

Taktfrequenz: 21-34 kHz

Der ernsthafte Wandler

 Zum Größenvergleich liegt oberhalb des Transformators eine Mignonbatterie. Der ernsthafte Trafo ist das Teil mit dem Hochspannungszeichen drauf. Die Primärspulen bestehen auf 2,5 mm² zweiadrigem Lautsprecherkabel. Jeweils sind das nur 3 Windungen für jede Primärspule, und die reichen bereits für die 24V aus! Durch die Verwendung einer 2-adrigen Leitung werden Symmetrie und Kopplung der beiden Primärspulen optimiert. Die Sekundärspule wurde mit Ø0,56mm Lackdraht gewickelt und ist vom Querschnitt her gut für 1 Ampere. Die Steuerwicklung mit der die beiden Transistorpaare umgeschaltet werden, besteht aus isolierter Schaltlitze, die nur einmal um den Kern gelegt wurde.

Oben und unten sieht man die beiden Kühlkörper, auf denen die Transistoren festgeschraubt sind. Diese Kühlkörper stammen von ausgedienten Solarladereglern. Die Transistoren von Typ BUV 27 sind sehr solide Arbeitstiere. Es wurden jeweils zwei Stück davon auf einem Kühlkörper montiert und mit den Emitterwiderständen aussymmetriert und parallel geschaltet um mehr Power zu haben.

In der Mitte thront die dicke L1. Dieses Trum von Spule von Hand zu wickeln, war übrigens eine ernsthafte Arbeit. Aber die Arbeit hat sich gelohnt. Die Spule benimmt sich hervorragend und versorgt den Transformator mit konstantem Strom.

Der rote Klotz unterhalb der Spule besteht aus den 4 Folienkondensatoren, die an die beiden Primärspulen angeschlossen sind. Sie wurden mit einem Tesa PowerStrip auf die Grundplatte geklebt. Im normalen Betrieb müssen diese Kondensatoren einen Strom von insgesamt ca. 20 Ampere aushalten und deshalb liegen hier auch 4 Stück parallel.

Die ganze Teile wurden entweder auf die Pertinax-Grundplatte geschraubt, geklebt, oder mit Kabelbindern festgezurrt. Die meisten Verbindungen wurden mittels Schrauben und Ringösen angeschlossen. Durch die wenigen und zentralen Kontaktpunkte und eine sternförmige Verdrahtung von den Versorgungsklemmen aus läuft die Schaltung sehr stabil und EMV-freundlich. :-)

Schaltplan  

(< zur Übersicht)

Stückliste

(< zur Übersicht)

Beschreibung des Ganzen

(< zur Übersicht)

Grundprinzip  und Berechnung dieses resonanten Gegentaktwandlers wurden bereits in dem Artikel über den kleinen Wandler ausführlich beschrieben, daher werden im Folgenden nur die wichtigsten Parameter und Eigenschaften behandelt. (Abgesehen davon erzähle ich viel lieber, als daß ich rechne. ;-)

Der ernsthafte Transformator  (< zur Übersicht)

Eines Tages fand ich an meinem Arbeitsplatz einen schönen großen Ferritkern vom Typ "PM62" von Siemens (heutiger Hersteller: EPCOS). Schon auf den ersten Blick war dieser Brocken wunderbar geeignet für einen leistungsstarken Resonanzwandler. 280 Gramm Gewicht sind für einen Ferritkern schon ganz ordentlich. Nun, niemand hatte mehr Verwendung für das Ding, also durfte es offiziell abgestaubt werden. :)

Der ernsthafte Transformator. (Zum Größenvergleich: eine Streichholzschachtel)

Daten des Trafokerns:

A_L = 315 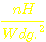; Luftspalt: 2,6mm

Eisenquerschnitt: A_e = 570mm²

Material: N27 (B_max= 200mT; f_max= 25kHz)

Primärspule:

2 * 3 Wdg. aus zweiadrigem 2,5mm² -Lautsprecherkabel. (gegensinnig gewickelt, d.h. eine "linksrum", die andere "rechtsrum")

Induktivität einer einzelnen Primärspule: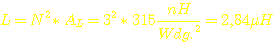

Induktivität beider Primärspulen: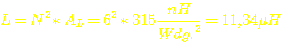

Sekundärspule:

165 Wdg. Ø 0,56mm Kupferlackdraht (CuL)

Induktivität der Sekundärspule: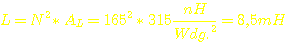

Betriebsdaten:

Nennfrequenz: 25 kHz (Leerlauffrequenz: 34 kHz)

Übersetzungsverhältnis Ü=55

Primär: 25V / 20 A

Sekundär: 1375V / 364 mA

Leistung: 500 VA   

Anmerkung: Auch bei diesem Trafo gilt, daß die Windungszahl der Sekundärspule das Übersetzungsverhältnis des Trafos bestimmt. Mit höheren Windungszahlen, können wenn gewünscht, auch deutlich höhere Ausgangsspannungen als diese 1,4kV erreicht werden. Bei Ferrit-Trafos, die mit einer hohen Frequenz betrieben werden, kommt man, anders als bei 50Hz-Transformatoren, schon mit relativ wenigen Windungen aus. Für den Bastler, bzw. Experimentator, der den Transformator selber wickeln will, ist das natürlich sehr angenehm.

Primärschwingkreis und Kondensatoren  (< zur Übersicht)

Die Kondensatoren im Primärkreis sind impulsfeste Folienkondensatoren vom Typ WIMA MKP10. Im Primärkreis fließt ständig ein recht großer Strom, weshalb leistungsstarke und verlustarme Kondensatoren benötigt werden.

Kondensatoren im Primärkreis

Anmerkung: Die schlechte Farbwiedergabequalität meiner Digitalkamera läßt diese Kondensatoren vermutlich etwas "tuffiger" erscheinen als vom Hersteller und auch von mir selber beabsichtigt.

Spannung an einer der Primärspulen: 25V (=Betriebsspannung der Schaltung).

Die Kondensatoren sind parallel zu den beiden in Reihe geschalteten Primärspulen angeschlossen und bekommen somit die doppelte Spannung ab, also 50V. Aus dem Datenblatt des Herstellers geht hervor, daß diese Kondensatoren bei 30 kHz ca. 90V und bei 40kHz ca. 70V aushalten. Wir haben also noch genügend Sicherheitsabstand.

Im Leerlaufbetrieb des Wandlers schwingt der Wandler auf:

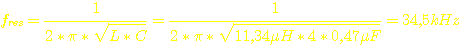
Für die 4 Kondensatoren C_ges = 4 * 0,47µF = 1,88µF ergibt das bei dieser Frequenz einen Blindwiderstand von: 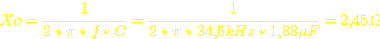. Das ist nicht gerade viel bei 50V... :o

Letztlich kriegen wir einen Strom von 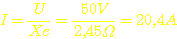 heraus. Diese 20A fließen wohlgemerkt nicht bei Vollast, sondern im Leerlauf! Im Lastbetrieb verringert sich die Frequenz des Wandlers, wenn auf der Sekundärseite ein Kondensator (zur Strombegrenzung oder auch eine Kaskade) angeschlossen wird. Bei geringerer Frequenz fließt also weniger Strom durch die Primärspule und die Kondensatoren, wodurch sich deren Streß verringert.

In dieser Schaltung kriegt also jeder Kondensator einen Wechselstrom von 20A / 4 = 5A ab. Das ist nicht gerade wenig. Der Knackpunkt bei der Belastung der Kondensatoren ist hier nicht die angegebene Spannung (630V= / 400V~), sondern der hohe Strom. Dieser Strom ergibt sich aus Kapazität, Frequenz und Spannung. Unter Anderem deshalb gibt der Hersteller solcher Kondensatoren sogenannte Derating-Kurven an in denen für jeden Kondensator die zulässige Spannung in Abhängigkeit der Frequenz angegeben wird.

Bitte nicht versuchen, diesen Schwingkreiskondensator mit kleinen (auch bipolaren) Elkos zu realisieren, "die doch auch funktionieren müßten", weil sie dieselbe Kapazität haben. Bei dieser hohen Strombelastung hätten solche Teile keine Chance mehr - hier müssen leistungsstarke Folienkondensatoren ran.

Transistor-Schaltstufen  (< zur Übersicht)

Schaltstufe auf Kühlkörper

Hier im Bild sieht man eine der beiden Schaltstufen. Beide Transistoren wurden mit Wärmeleitpaste (Arctic Silver 3, was sonst? ;-) aber ohne Isolierscheibe versehen. Dadurch wird der Wärmeübergang vom Transistorgehäuse zum Kühlkörper optimiert und eine elektrische Isolation ist ohnehin nicht nötig. Die Kollektoren (an den Kühlfahnen) der Transistoren sind also schon über den Kühlkörper miteinander verbunden, aber das macht nichts, da die beiden BUV27 ohnehin parallel geschaltet sind. Dadurch daß die Kühlkörper auf Betriebspannungspotential liegen, dürfen sie nicht auf ein gemeinsames, leitfähiges Chassis montiert werden. Die Berührungssicherheit ist jedoch, da die Schaltung mit Schutzkleinspannung betrieben wird, immer noch gewährleistet.

Die Transistoren, die hier zum Einsatz kommen, sind wieder die BUV27, die schon im kleinen Wandler zum Einsatz kamen. Deren Verstärkung ist "ordentlich" (Angabe über Stromverstärkung h_fe fehlt leider im Datenblatt) und die Sättigungsspannung ist schön niedrig (0,7V bei 4A Kollektorstrom).

Für jede Schaltstufe an den Primärspulen des Transformators wurden zwei dieser Transistoren parallel geschaltet, um mehr Power in den Trafo pumpen zu können. Bei einer Parallelschaltung von Bipolartransistoren (npn oder pnp) müssen, anders als bei MOSFETS, die Transistoren symmetriert werden. Ohne diese Symmetrierung mit den Emitterwiderständen R1-R4 würden die Transistoren ungleich belastet. Im Extremfall kann das dazu führen, daß einer der Transistoren abraucht, während der andere nur lauwarm ist.

Ein Bipolartransistor hat einen negativen Temperaturkoeffizienten, daß heißt er wird niederohmiger wenn er wärmer wird. Schaltet man ohne Symmetrierung zwei solcher Transistoren parallel, so wird aufgrund der Toleranzen dieser Bauteile einer der beiden Transistoren etwas mehr Strom abbekommen als der andere. Durch diesen etwas höheren Strom wird sich dieser "bessere" Transistor stärker erwärmen als der andere -> er wird noch niederohmiger und bekommt noch mehr Strom ab -> er wird noch heißer und niederohmiger ... bis er an Überhitzung stirbt. Ist dieser eine Transistor dann vollständig ausgefallen (hochohmig), bekommt der zweite, ihm parallel geschaltete, Transistor den vollen Strom ab... bis auch er verdunstet. Grund genug, diese Widerstände einzubauen, wenn sie auch den Wirkungsgrad des Wandlers verschlechtern.

Die Emitterwiderstände (0,15 Ohm / 5W) funktionieren folgendermaßen: Wenn jetzt, wie in obigem Absatz beschrieben, ein Transistor etwas mehr (Kollektor-)Strom leiten "will" als der andere, so fließt dieser höhere Strom auch durch dessen Emitterwiderstand und es entsteht ein erhöhter Spannungsabfall an ihm. Dieser Spannungsabfall wirkt der Basisspannung des Transistors entgegen, verringert sie, und reduziert dadurch über den Basisstrom auch wieder den Kollektorstrom. Der Transistor wird gewissermaßen "ausgebremst".

Dieses "Ausbremsen" wirkt sich bei beiden parallelen Transistoren gleich aus. "Will" einer davon aufgrund von Bauteiletoleranzen oder Temperaturunterschieden mehr Strom leiten als der andere, wird er durch den Spannungsabfall am Emitterwiderstand zugedreht und der andere Transistor wird im selben Zug etwas weiter aufgedreht. Auf diese Weise werden die Ströme durch beide Transistoren aneinander angeglichen, also symmetriert.

An jedem der Emitterwiderstände fällt bei maximalem Strom (5A) eine Spannung von 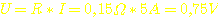ab. Dieser Spannungsabfall erzeugt zusammen mit dem Strom eine Verlustleistung von . Die Widerstände werden also nicht überlastet.

Der maximale Eingangsstrom dieses Wandlers liegt bei 20 Ampère. Dieser Strom verteilt sich (im Mittelwert) auf beide Schaltstufen, und dort verteilt er sich wiederum auf zwei Transistoren. So bekommt jeder der Transistoren ein Viertel des Stromes, also 5A ab. Nehmen wir an, einer der Transistoren hätte eine Kollektor-Emitter-Sättigungsspannung von 0,9V, dann ergibt sich pro Transistor eine Verlustleistung von 0,9V * 5A = 4,5W. Hieraus ergibt sich, daß jeder Kühlkörper in der Lage sein muß, 9W  abzuführen, ohne daß die Transistoren überhitzen. Geschätzt würde ich sagen, daß Kühlkörpern mit ca. 3 K/W ausreichen sollten.

(Sorry, aber die genaue Kühlkörperberechnung spare ich mir hier. Erstens habe ich hier eine solche ohnehin nicht durchgeführt und zweitens vertraue ich meiner Schätzung so lange, bis die Transistoren glühen. Wenn die Geschichte zu heiß wird, montiere ich einfach Lüfter. ;-)

Die Basisvorwiderstände R5,R6 (470 Ohm, 0,5W) wurden hinprobiert. Ohne Angabe der Stromverstärkung der Transistoren im Datenblatt bleibt einem auch kaum etwas anderes übrig.

Insgesamt erzeugen die Schaltstufen mit den 4 Transistoren und Emitterwiderständen bei Vollast des Wandlers eine Verlustleistung von 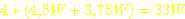. Das klingt zwar nach viel, ist aber gemessen an der Nennleistung des Wandlers von 500 VA durchaus noch akzeptabel. In Prozent ausgedrückt, werden 6,6% der gesamten Leistung in den Schaltstufen verheizt. (Basisströme der Transistoren sind hierbei noch nicht berücksichtigt)

Die dicke L1  (< zur Übersicht)

Entstanden ist diese Spule folgendermaßen:

Ein Arbeitskollege von mir fand in seinem Teile-Sammelsurium einen schönen, größen Eisenpulverkern und meinte: "Das ist doch was für Dich!" Auf diese Aussage erntete er meine volle Zustimmung, wodurch ich in den Besitz dieses T250-40 - Kerns gelangte. Sodenn griff ich mir eine "nennenswerte Menge" 1,5mm-Lackdraht, welcher mir sehr ernsthaft vorkam und verbrachte zwei Feierabende damit, diesen Draht durch den Kern zu wickeln. Spulen wickeln hat, bei eintsprechender persönlicher Neigung, einen gewissen meditativen Aspekt... "Eins" - "Ommmm" - "Zwei" - "Ommmm" - "Drei" - ...  Ein sehr entspannender Job für den, der's mag. Diese Spule entstand, als der ernsthafte Wandler noch nicht einmal in Planung war. Um so besser, daß sich diese Meditationsarbeit nun auch aus technischer Sicht gelohnt hat. :)

Die Drosselspule L1 hat jedenfalls die Aufgabe, den Transformator an der Mittelanzapfung der Primärwicklungen mit konstantem (Gleich-) Strom zu versorgen, bzw. die Wechselspannung die an diesem Punkt anliegt von der Stromversorgung fernzuhalten (zu entkoppeln). Je höher die Induktivität dieser Spule ist, desto weniger von der Wechselspannung am Trafo kommt bis zu den Anschlüssen für die Versorgungsspannung "durch".

Drosselspule L1

Je höher die Induktivität, desto "gleicher" wird der Strom der sie durchfließt, oder anders ausgedrückt: Die Restwelligkeit des Stromes wird verringert. Wählt man die Induktivität so groß, daß diese Restwelligkeit vernachlässigbar klein wird, bekommt der Kern der Spule fast kein Wechselfeld mehr ab und wird fast ausschließlich mit einem Gleichfeld magnetisiert. Ist das Wechselfeld im Spulenkern sehr schwach, kann man einen Kern aus sehr preiswertem Niederfrequenzmaterial verwenden, da ohnehin kaum Wirbelströme auftreten können. Anstelle des hier verwendeten Eisenpulver-Ringkerns ginge hier auch ein Kern aus Trafoblech oder sogar aus massivem Eisen.

Wichtig bei diesem Spulenkern ist aber, daß er einen Luftspalt besitzt. Der Luftspalt bewirkt als magnetischer Widerstand, daß sich der Kern nicht so leicht in die magnetische Sättigung treiben läßt. Wäre der Kern magnetisch gesättigt, wäre er magnetisch nicht mehr wirksam und die Spule würde dann den größten Teil ihrer Induktivität verlieren, wodurch sie als Stromkonstanthalter und Filter ausfallen würde.

Der hier verwendete Kern T250-40 des Herstellers Micrometals besteht aus feinem Eisenpulver, das mit einer Kunststoffmasse zu einem soliden Ring verbacken wurde. Der kunststoffgefüllte Zwischenraum zwischen den Eisenpartikeln im Kernmaterial schafft einen verteilten (Luft-)Spalt, und so ist dieses Material hervorragend für Drosselspulen geeignet. Das "T" in der Typenbezeichnung des Kerns steht für "Toroid", die "250" geben den Außendurchmesser in Hundertstel Zoll an (2,5 Zoll = 63,5mm), und die "40" kodieren das Kernmaterial. Das 40-er Material ist übrigens das billigste, das es von diesem Hersteller gibt. Üblicherweise verwendet man solche Kerne für Netzdrosseln und andere 08/15-Anwendungen.

Berechnung der real existierenden Spule (< Zurück zu: Hauptüberschrift / Übersicht )

In diesen Kern wurden ca. 116 Windungen Kupferlackdraht mit 1,5mm Durchmesser hineingewickelt. Übrigens... Ringkerne zu bewickeln, vor allem mit so dickem Draht, ist etwas langwierig und recht anstrengend für die Finger. Für jede Windung muß die gesamte Drahtlänge durch das Loch im Kern gezogen werden. Die Drahtlänge kann grob berechnet werden, indem man die Länge einer einzigen Windung durch Messung der mechanischen Abmessungen des Kerns ermittelt und diese Länge dann mit der Windungszahl multipliziert. Der Kern hat eine Höhe von 25,4mm und eine Materialstärke von 15,85mm, also ist eine einzige Windung: 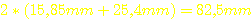lang. Für die ganze Spule werden 161 Wdg. * 82,5mm = 13,3m Draht benötigt.

 Okay, nachdem diese Spule schon nicht im Voraus berechnet wurde, dann mach' ich's eben jetzt.

Der Ø1,5 mm Draht hat nach meinem alten Tabellenbuch einen Querschnitt von 1,767mm² und einen spezifischen Widerstand von 9,93 Ohm/km. Also haben diese 13,3m einen Widerstand von 0,132 Ohm. Diese Werte kann man übrigens auch zu Fuß über den spezifischen Widerstand von Kupfer und den Drahtquerschnitt ausrechnen, aber das sei hier nur der Vollständigkeit halber erwähnt. Würde man 20A über diese Spule schicken, ergäbe sich ein Spannungsabfall von U = R * I = 0,132 Ohm * 20 A = 2,64V. Die Verlustleistung wäre dann: P = U * I = 2,64V * 20A = 52,8W (auweia!). Ergebnis dieser Berechnung: Würde also man tatsächlich 20 A durch diese Spule jagen, würde sie wohl anfangen zu dampfen. (Mistikack!) Nun ja, ein weiteres Wunder ist dieses Ergebnis nicht. Die Stromdichte betrüge in diesem Fall 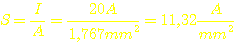, läge also weit über den üblichen Faustwerten von 2 .. 5A / mm². Wenn der ernsthafte Wandler also einmal mit der (bisher nur theoretischen) Maximalleistung betrieben werden soll, muß diese Spule neu berechnet und gewickelt werden.

Für die Induktivität gilt: L= N² * A_L = 116Wdg.² *194 nH/Wdg. = 2,61 mH (siehe auch: Datenblätter der Kerne von Micrometals)

L = Induktivität in Henry

N = Windungszahl (ohne Einheit)

A_L = A_L -Wert des Kerns

Für die magnetische Flußdichte im Kern gilt: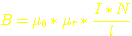

B = Flußdichte in Tesla

µ₀ = magnetische Feldkonstante (Naturkonstante) = 1,257 * 10^-6 =

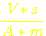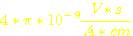
µ_r = materialabhängige Permeabilitätszahl (ohne Einheit). hier: 60

I = Strom durch die Spule in Ampère. hier gewählt: 20A

l = mittlere Feldlinienlänge (Eisenweglänge) in Meter. hier: 0,15m

Dann kriegen wir eine Flußdichte von 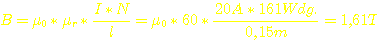(autsch!)

Um herauszufinden, warum dieses "autsch", schauen wir mal im Datenblatt die Graphen zu Initial Permeability vs. DC Magnetizing Force Graph an um herauszufinden, wie stark denn dieses 40er - Material überhaupt magnetisiert werden darf. Der Hersteller gibt bei diesen Kurven nicht das "B" (Flußdichte) an, sondern das "H" (Feldstärke).

Die Feldstärke berechnet sich folgendermaßen: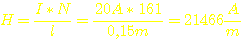

Schauen wir nun in obengenanntes Schaubild, so sind wir immer noch nicht viel schlauer. Micrometals, als traditionsbewußtes, amerikanisches Unternehmen, rechnet wie andere Firmen in diesem Lande immer noch mit jungsteinzeitlichen Maßeinheiten wie z.B. Füßen (foot), Daumenbreiten (inch) und Pfunden. In dieser Kurvenschar z.B. geben sie die magnetische Feldstärke in Öhrchen (Oersteds) an. Diese (nicht mehr zulässige) Einheit muß erst noch in eine richtige Maßeinheit umgerechnet werden, andersrum geht's natürlich auch.

Hierbei gilt: 1 Oe = 0,7958 A/cm = 79,58 A/m

Jetzt können wir endlich die Feldstärke in Örsted ausrechnen: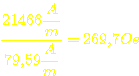

Anhand der Graphen, die der Hersteller angibt, erkennt man, daß bei diesem Strom fast keine Permeabilität (µ_r) mehr vorhanden ist. Bei I=20A ist also dieser Spulenkern schon total in der Sättigung und von der oben berechneten Induktivität (2,6mH) ist nicht mehr viel übrig.

Betreibt man den ernsthaften Wandler hingegen nur bei 5A, ist die Feldstärke in der L1 auch nur ein Viertel so groß wie bei 20A. Das wären dann 269,7 Oe / 4 = 67,4 Oe. Im zugehörigen Graphen für das 40er - Material liest man ab, daß bei dieser Feldstärke das Material noch eine Permeabilität von µ_r = 30 hat. Demnach hat diese Spule bei einem Strom von 5A auch keine 2,6mH mehr, sondern nur noch die Hälfte, also 1,3 mH, (Die Permeabilität hat sich halbiert, also halbiert sich auch die Induktivität) was aber immer noch dicke ausreicht.

 Wie komme ich eigentlich drauf, daß das dicke ausreicht? Nun, der Job dieser Spule ist es ja, zu verhindern, daß Wechselstrom von Trafo zu Versorgung zurückfließen kann. Der Wandler schwingt im Lastbetrieb auf ca. 21kHz. Bei dieser Frequenz hat eine 1,3mH-Spule einen Blindwiderstand von 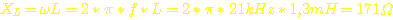. Über der Spule fällt eine Wechselspannung in Höhe der Versorgungsspannung des Wandlers ab, also U~ = 25V.

Nach dem ohmschen Gesetz fließt bei dieser Spannung und diesem Blindwiderstand ein Wechselstrom von: .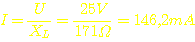

Dieser Strom, der dem Elektrolytkondensator C₁ aufgebrummt wird, stellt überhaupt kein Problem dar. Dieser ist ein Alupott mit 15.000µF, für dessen Topfgröße diese knappen 150mA immer noch lächerlich wenig sind. (Ein solches Teil hält üblicherweise mehrere Ampere aus. Da ich für diesen alten Elko kein passendes Datenblatt mehr finde, muß diese Schätzung eben ausreichen).

Okay, das war nun die "Rückwärts"-Rechnung. Wie also würde man eine solche Spule korrekt dimensionieren? Das kommt im nächsten Kapitel.

Berechnung der korrekten Spule (< Zurück zu: Hauptüberschrift / Übersicht )

Sagen wir mal, wir lassen einen Wechselanteil beim Strom durch die Spule von 1A zu. Dann brauchen wir eine Spule, die bei Vollastbetrieb (20A) und der Betriebsfrequenz von 21kHz einen Blindwiderstand von 25V / 1A = 25 Ohm hat. Mit der Formel für den Blindwiderstand von Spulen 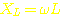=> 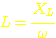kommen wir auf 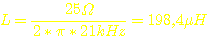. Sagen wir der Einfachheit halber: L=200µH.

Den Leerlauf-Fall des Wandlers, in dem er auf einer höheren Frequenz schwingt, brauchen wir hier nicht gesondert zu betrachten. Bei höherer Frequenz ist auch der Blindwiderstand der Spule höher, wodurch sie noch weniger Wechselstrom durchläßt.

 Mit diesem Kern, der einen A_L-Wert von 194 nH/Wdg.² hat, brauchen wir nach der Formel für die Induktivität 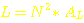=> 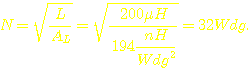Na, das ist doch noch sehr angenehm zu wickeln. :-)

Für die Feldstärke im Kern heißt das dann: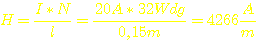

Dieser Wert in Oersted: 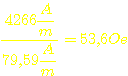. Das ist immer noch etwas viel.

Die Permeabilität dieses Kernmaterials ist bei 53,6 Oe schon auf µ_r = 35 abgesunken. Das heißt, die ursprüngliche Berechnung der Windungszahl (mit N=32) paßt hier schon wieder nicht mehr. Mit dem µ_r sinkt ja auch der A_L - Wert. Spätestens jetzt sieht man, daß die Dimensionierung einer Spule ein ständiges hin- und her - rechnen ist. Nehmen wir jetzt eine höhere Windungszahl, damit auch bei hoher Strombelastung noch eine ausreichende Induktivität vorhanden ist, dann wird dadurch auch wieder die magnetische Feldstärke im Kern erhöht, wodurch das µ_r wieder sinkt. Diese Rechnerei beißt sich also ständig selber in den Ar.. -äh- Hintern. Es ist ein ständiges Herumprobieren nötig - solange eben, bis man auf akzeptable Werte kommt. Dazu ist noch zu sagen, daß für andere Anwendungen von Spulen schon wieder andere Parameter angelegt werden müssen. Da die Spule, die hier benötigt wird, nicht mit einem starken Wechselfeld belastet wird, wirkt es sich nicht ganz so fatal aus, wenn der Kern in die Nähe der Sättigung kommt. Wäre die Feldstärke von 4266 A/m kein Gleich- sondern ein Wechselfeld, wie es in vielen anderen Anwendungen der Fall ist, so wäre der Kern hier schon hemmungslos überlastet und würde durch die sehr hohen Ummagnetisierungsverluste schweineheiß werden. Nur gut, daß das bei einem Gleichfeld nicht passiert (Der Kern wird nicht ummagnetisiert, bzw. die Richtung der Magnetisierung bleibt hier immer gleich). Der Wechselanteil des Magnetfeldes in unserer Spule hier ist sehr gering.

Also gut... Schätzen wir mal die Windungszahl auf N = 50... Dann kriegen wir:

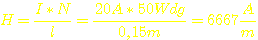= 83,8 Oe ; Hier hat der Kern noch ein µ_r von 25.

µ_r und A_L- Wert hängen linear voneinander ab. Daher ist der A_L- Wert jetzt 194 * (25 / 60) = 80,83 nH / Wdg.²

Die Induktivität bei Vollast liegt jetzt also bei L = N² * A_L = 50 Wdg.² * 80,83 nH / Wdg.² = 200µH.

Diese 200 µH passen jetzt wunderbar zu unserer Vorgabe von oben. - Glück gehabt! ;-)

Okay, wenn wir's jetzt schaffen, diese 50 Wdg. Draht mit einem nennenswerten Querschnitt (ca. 2,5mm²) in den Kern zu wickeln, haben wir eine Spule, die auch bei Vollast des ernsthaften Wandlers weder anfängt zu dampfen, noch zu viel von ihrer Induktivität verliert.

Inbetriebnahme   (< zur Übersicht)

(Nachtrag 5.1.2003) Einige Leute, die diesen Wandler nachgebaut haben, hatten Schwierigkeiten mit dessen Inbetriebnahme. Dieser Nachtrag soll diese Schwierigkeiten beseitigen. Wenn ihr also den Wandler nachgebaut habt, macht erst mal Folgendes...

Das allererste Mal:  (< Zurück zu: Hauptüberschrift / Übersicht )

Der ernsthafte Wandler wird an ein strombegrenztes Netzgerät angeschlossen. Dieses wird auf 12V Ausgangsspannung und ca. 1A Strombegrenzung eingestellt. Ist der Wandler korrekt aufgebaut, sollte er mit dieser Versorgung schon gut arbeiten und am Ausgang des Wandlers sollten ca. 700V anliegen. Hätte der Wandler bei diesem ersten Anschließen noch einen Fehler, bringt ihn dieses eine Ampere sicher noch nicht um.

Am Besten mißt man die Ausgangsspannung des Wandlers mit einem Oszilloskop. Sieht man am Ausgang des Trafos eine schöne Sinuskurve im Frequenzbereich von 30-35 kHz (im Leerlauf) mit der korrekten Spannung, dann ist alles paletti ! Bei der Messung der Ausgangsspannung muß ein Hochspannungstastkopf für das Oszilloskop verwendet werden. Ist ein solcher nicht vorhanden, kann man auf der Primärseite (Niederspannungsseite) messen, und zwar am Besten direkt an den äußeren Enden der Primärspule. Sieht man hier einen schönen Sinus, ist zumindest der Niederspannungsteil des Wandlers in Ordnung.

Anschluß des Transformators: (< Zurück zu: Hauptüberschrift / Übersicht )

Fast alle Probleme, die bei der ersten Inbetriebnahme auftreten, kommen daher, daß der Transformator falsch angeschlossen, bzw. gewickelt wurde.

Symptome für solche Fehler: Wilde Schwingungen auf viel zu hoher Frequenz, hohe Stromaufnahme, schlechter Wirkungsgrad, geringe Ausgangsleistung, geringe Ausgangsspannung.

Primärwicklungen:

Diese müssen, elektrisch gesehen, gegensinnig auf den Trafo gewickelt sein. Ist eine der beiden Primärwicklungen falsch herum angeschlossen, wird der Ferritkern nur in eine Richtung magnetisiert und der Wandler kann nicht korrekt arbeiten.

Man kann hierfür tatsächlich eine der beiden Primärwicklungen (3 Wdg. 2,5mm²) linksherum und die andere rechtsherum wickeln, dies ist aber eher umständlich. Da für den Transformator nur wichtig ist, daß die beiden Spulen ein Magnetfeld von jeweils anderer Richtung erzeugen, kann man diese beiden Wicklungen auch bifilar (parallel, gemeinsam) wickeln, und dann eine davon außerhalb des Trafos elektrisch umpolen. Es ist ratsam, für diese Wicklung eine dicke, zweiadrige Leitung (Lautsprecherkabel) zu verwenden. Da beide Adern solcher Leitung mechanisch miteinander verbunden sind, werden beide Primärwicklungen identisch in Drahtlänge und Kopplung zum Kern. Dadurch wird der Transformator im Betrieb symmetrisch ausgesteuert und der Wandler kann optimal arbeiten.

Steuerwicklung:

Diese "Wicklung", die nur aus einer einzelnen Windung besteht, ist dafür zuständig, die richtige Transistor-Schaltstufe zum richtigen Zeitpunkt (Phasenlage) einzuschalten. Wenn der Wandler nicht richtig arbeitet, obwohl die Primärspule korrekt ist: einfach mal die beiden Enden der Steuerwicklung vertauschen. ;-)

Man verzeihe mir, daß ich nicht jede Trafowicklung in der Schaltungsbeschreibung korrekt mit Wicklungsanfängen und -enden angegeben habe, aber o.g. Hinprobiermethode ist einfach bequemer und geht schneller. Die einzige Wicklung, deren korrekte Polarität hinprobiert werden muß, ist die Steuerwicklung. Viel umständlicher wäre es gewesen, beim Wickeln des Trafos bei den Wicklungen auf Anfang, Ende, Wickelsinn, Anschluß an den Pins (Polung) zu achten. Sorry, aber hier war ich faul. :p

Vorsicht bei den Messungen!

Solange der Wandler nur mit 12V versorgt wird, tritt auf der Niederspannungsseite keine gefährlich hohe Spannung auf, man kann hier also gefahrlos messen (ohne Gewähr!). Wichtig ist, daß man nicht während des Herumprobierens an die Ausgangs-Pins des Transformators kommt. Hier kann eine sehr hohe Spannung anliegen, über deren Gefährlichkeit ich mich hier vermutlich nicht mehr auslassen muß.

Nachwort   (< zur Übersicht)

Hiermit definiere ich die Beschreibung des ernsthaften Wandlers als abgeschlossen. Auch wenn jemand nicht dieses konkrete Gerät nachbauen will, so hoffe ich, daß derjenige doch einen gewissen Einblick in die Technologie solcher Wandler, sowie in das Berechnen und Auslegen von Spulen gewinnen konnte.

Induktive Bauelemente sind für viele Elektroniker entweder rote Tücher oder Bücher mit sieben Siegeln. Ich hoffe, mit obigen Berechnungen und Beispielen gezeigt zu haben, daß das nicht so sein muß. Hat man sich erst einmal an diese Bauelemente mit ihren Eigenschaften gewöhnt, ist man auf einmal ganz wild drauf. :-D Spulen haben insofern eine Sonderstellung als sie in vielen Fällen selbst hergestellt werden müssen, bzw. können. Alle anderen Bauteile gibt es fertig von der Stange. Aus diesem Grunde muß man eben etwas in die Spulentechnik einsteigen, wenn man solche Bauteile erfolgreich verbauen will.

Viel Spaß! :-)

zum Seitenanfang